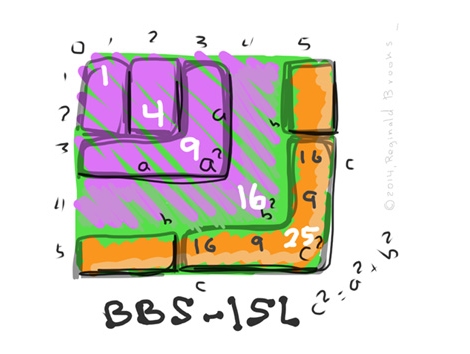
There is a simple whole number (integer) matrix grid table upon — and within — that every possible whole number Pythagorean Triangle — a.k.a. Pythagorean Triple — can be placed, and proved. The Brooks Base Square - Inverse Square Law (BBS-ISL) matrix is an infinitely expandable grid that reveals ALL Pythagorean Triples — both Primitive Triples (PPT) and their non-Primitive multiples (nPTT). An extremely simple geometric AREA proof of the Pythagorean Theorem — c2=a2+b2 — is built into the BBS-ISL matrix.
Not only does the Inverse Square Law describe, define and quantify our most important energies (and their expressions as force)— gravity, light, sound, electromagnetism... — the BBS-ISL matrix grid is composed of Pythagorean Triples crisscrossing over much of the entire grid. An intimate inter-connection way beyond a simple, casual association has been revealed. The Dickson Method confirms, validates and provides insight into the generation of ALL Pythagorean Triples. Please see the TPISC project white paper for the full mother load.
Full Description
There are two parts to TPISC: The Pythagorean — Inverse Square Connection ~A MathspeedST Supplement~:
- INTRO to TPISC (This Overview)
- TPISC (white paper)
In this INTRO to TPISC, you get a greatly simplified introduction and overview of TPISC: The Pythagorean — Inverse Square Connection white paper.
The actual white paper (TPISC) is packed full of visual media, charts and tables to follow the process of discovery. The relationships — connections and inter-connections — between the BBS-ISL matrix and the Pythagorean Theorem (as Pythagorean Triples) is so vast that the process of simplifying it down to consistent, irrefutable and concrete visuals became the motivation and driving force of this entire project.
What is so amazing about the BBS-ISL matrix?
If you scan each Row/Column, only some have squared numbers. If they do, the squared numbers always come in pair-sets. In every case, those square number pair-sets are the AREAS of the two shorter sides ("a" and "b") of a Pythagorean Triple triangle. The longer hypotenuse (c) AREA is located on the Prime Diagonal — the diagonal line dividing the matrix grid evenly into two symmetrical halves!
This is their story.
Work metadata
- Year Created: 2014
- Submitted to ArtBase: Monday Aug 18th, 2014
- Original Url: http://www.brooksdesign-ps.net/Reginald_Brooks/Code/Html/MSST/TPISC/BBS_Pythag_netart17/BBS_Pythag_netart17.html
-
Work Credits:
- reginaldbrooks, primary creator
Take full advantage of the ArtBase by Becoming a Member
Artist Statement
Right next to Einstein's E=mc2, and, the diminishing influence with distance relationship know as the Inverse Square Law (ISL), the Pythagorean Theorem — c2=a2+b2 — is probably one of the most well known mathematical statements. (Not counting simple formulas.)
It certainly is one of the oldest. Thousands of years ago, a string with knots at 3 units, followed by 4 more units, followed by 5 more units, when closed up, was found to form a perfect 3-4-5 right-angle triangle. Game on!
While Pythagorean Triangles can be formed with both whole and fractional numbers, it is with whole number integers (1,2,3...) — like in the 3-4-5 triangle — that they shine light on their relationships to other geometric forms and subsequent mathematical ideas!
Pythagorean Triangles that are composed solely of whole number integers are called Pythagorean Triples (PTs).
Some PTs — like the 3-4-5 — are as reduced and simple as they can get. Others are multiples of the simple primitive PTs. For centuries now, efforts have been made to identify ALL of them — primitives and non-primitives (multiples), alike. Along the way, thousands of proofs of the Pythagorean Theorem have issued forth.
In July of 2014, TPISC: The Pythagorean — Inverse Square Connection ~A MathspeedST Supplement~ — was introduced. ALL Pythagorean Triples and their proofs are directly visible right on — within, really — that symmetrical, expanding grid of whole numbers describing the Inverse Square Law: The BBS-ISL matrix.
TPISC is a natural, built-in relationship within the very foundational core of the BBS-ISL matrix. Come see for yourself!